Garis Sumbu Adalah sangat penting dalam geometri karena dapat digunakan untuk menentukan sifat-sifat segitiga, seperti simetri, luas, dan keliling. Garis ini juga dapat digunakan untuk menyelesaikan berbagai masalah geometri, seperti mencari panjang sisi atau sudut sebuah segitiga.
Garis Sumbu Adalah pertama kali ditemukan oleh matematikawan Yunani kuno, Euclid, pada abad ke-3 SM. Euclid menggunakan garis ini untuk membuktikan berbagai teorema geometri, termasuk teorema Pythagoras.
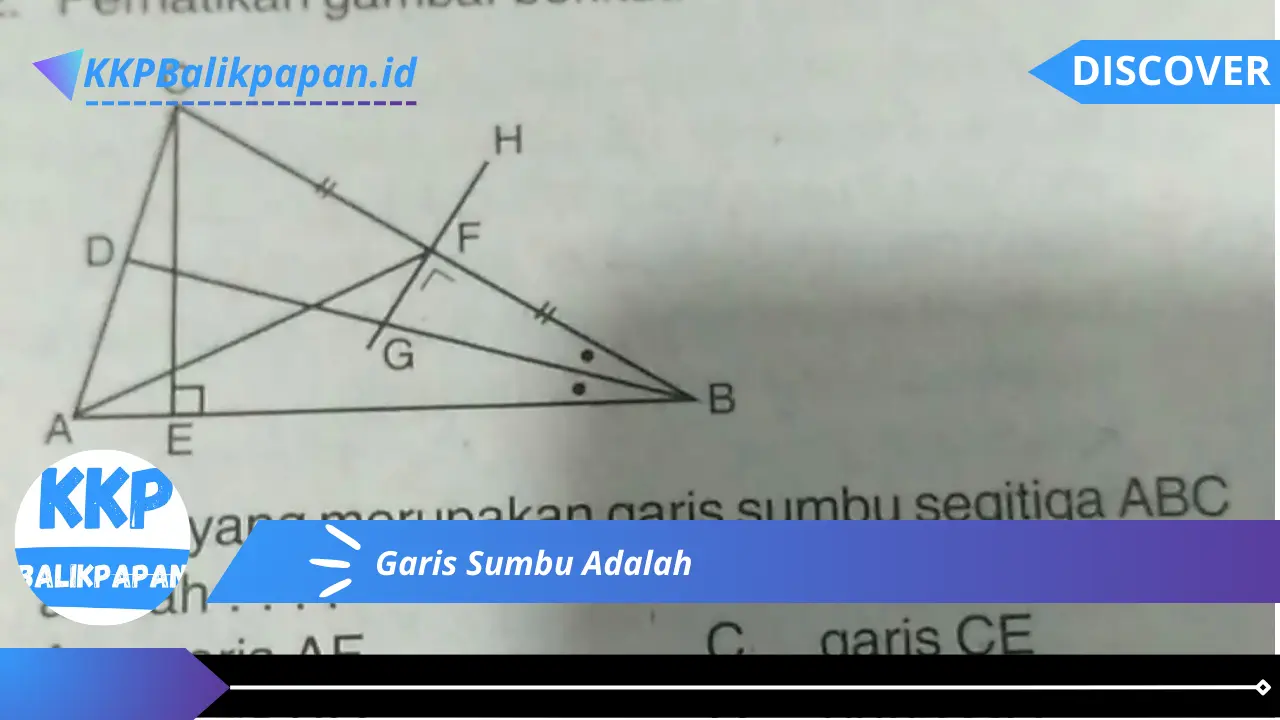
Garis Sumbu Adalah
Garis Sumbu Adalah merupakan salah satu konsep dasar dalam geometri yang memiliki peran penting dalam menentukan sifat-sifat segitiga. Berikut adalah tujuh aspek penting yang terkait dengan Garis Sumbu Adalah:
- Definisi: Garis yang menghubungkan titik puncak segitiga dengan titik tengah sisi dasarnya.
- Fungsi: Membagi segitiga menjadi dua bagian yang sama besar.
- Sifat: Memotong sisi dasar segitiga tegak lurus.
- Penggunaan: Menentukan titik berat segitiga.
- Rumus: Panjang garis sumbu adalah setengah dari panjang sisi dasar.
- Sejarah: Pertama kali ditemukan oleh Euclid pada abad ke-3 SM.
- Aplikasi: Digunakan dalam berbagai masalah geometri, seperti mencari luas dan keliling segitiga.
Ketujuh aspek ini saling terkait dan membentuk pemahaman yang komprehensif tentang Garis Sumbu Adalah. Definisi dan fungsi garis sumbu menjadi dasar untuk memahami sifat dan penggunaannya. Rumus dan sejarah memberikan informasi tambahan tentang aspek teknis dan perkembangan konsep ini. Terakhir, aplikasi garis sumbu menunjukkan relevansinya dalam menyelesaikan masalah geometri praktis.
Definisi
Definisi ini secara jelas dan ringkas menjelaskan konsep Garis Sumbu Adalah. Garis yang menghubungkan titik puncak segitiga dengan titik tengah sisi dasarnya merupakan ciri khas dari garis sumbu. Definisi ini menjadi dasar untuk memahami sifat-sifat dan penggunaan garis sumbu dalam geometri.
Dari definisi tersebut, dapat disimpulkan bahwa garis sumbu selalu melalui titik berat segitiga. Titik berat adalah titik potong ketiga garis sumbu pada sebuah segitiga. Hal ini menunjukkan bahwa garis sumbu memiliki peran penting dalam menentukan keseimbangan dan kestabilan segitiga.
Selain itu, definisi garis sumbu juga berkaitan dengan sifat simetri segitiga. Garis sumbu membagi segitiga menjadi dua bagian yang sama besar dan kongruen. Sifat simetri ini menjadi dasar untuk membuktikan berbagai teorema geometri, seperti teorema sudut dasar sama kaki.
Fungsi
Fungsi garis sumbu yang membagi segitiga menjadi dua bagian yang sama besar memiliki beberapa implikasi penting:
- Menentukan titik berat segitiga: Titik berat segitiga adalah titik potong ketiga garis sumbu. Karena garis sumbu membagi segitiga menjadi dua bagian yang sama besar, maka titik berat membagi garis sumbu menjadi dua bagian yang sama panjang.
- Membuktikan teorema geometri: Fungsi garis sumbu yang membagi segitiga menjadi dua bagian yang sama besar digunakan untuk membuktikan berbagai teorema geometri, seperti teorema sudut dasar sama kaki. Teorema ini menyatakan bahwa sudut-sudut dasar segitiga sama kaki sama besar.
- Menghitung luas dan keliling segitiga: Fungsi garis sumbu dalam membagi segitiga menjadi dua bagian yang sama besar dapat digunakan untuk menyederhanakan perhitungan luas dan keliling segitiga. Dengan mengetahui panjang garis sumbu dan salah satu sisi alas, luas dan keliling segitiga dapat dihitung dengan mudah.
Dengan demikian, fungsi garis sumbu yang membagi segitiga menjadi dua bagian yang sama besar memiliki peran penting dalam geometri untuk menentukan sifat-sifat segitiga, membuktikan teorema, dan menghitung luas dan kelilingnya.
Sifat
Sifat garis sumbu yang memotong sisi dasar segitiga tegak lurus memiliki beberapa implikasi penting:
Pertama, sifat ini menunjukkan bahwa garis sumbu selalu melalui titik tengah sisi dasar. Hal ini karena garis yang tegak lurus terhadap sisi dasar dan melalui titik puncak segitiga hanya dapat berpotongan dengan sisi dasar pada titik tengahnya.
Kedua, sifat ini berkaitan dengan simetri segitiga. Garis sumbu yang tegak lurus terhadap sisi dasar membagi segitiga menjadi dua bagian yang kongruen. Hal ini karena kedua bagian tersebut memiliki alas yang sama (setengah dari sisi dasar) dan tinggi yang sama (jarak dari titik puncak ke sisi dasar).
Ketiga, sifat ini dapat digunakan untuk menentukan panjang garis sumbu. Panjang garis sumbu sama dengan setengah dari panjang sisi dasar, karena garis sumbu membagi sisi dasar menjadi dua bagian yang sama panjang.
Dengan demikian, sifat garis sumbu yang memotong sisi dasar segitiga tegak lurus memiliki peran penting dalam menentukan sifat-sifat segitiga, membuktikan teorema, dan menghitung panjang garis sumbu.
Penggunaan
Garis Sumbu Adalah memiliki peran penting dalam menentukan titik berat segitiga. Titik berat segitiga adalah titik potong ketiga garis sumbu pada segitiga tersebut. Garis sumbu yang membagi segitiga menjadi dua bagian yang sama besar, memastikan bahwa titik berat terletak pada garis sumbu tersebut.
Untuk menentukan titik berat segitiga menggunakan Garis Sumbu Adalah, dapat dilakukan langkah-langkah berikut:
- Gambarlah garis sumbu pada segitiga.
- Bagi garis sumbu menjadi dua bagian yang sama panjang.
- Titik bagi garis sumbu tersebut adalah titik berat segitiga.
Mengetahui titik berat segitiga sangat berguna dalam berbagai aplikasi, seperti:
- Menentukan keseimbangan dan kestabilan segitiga.
- Menghitung momen inersia segitiga.
- Mencari pusat massa benda yang berbentuk segitiga.
Rumus
Rumus ini merupakan salah satu sifat penting dari Garis Sumbu Adalah yang menghubungkan panjang garis sumbu dengan panjang sisi dasar segitiga. Rumus ini menyatakan bahwa panjang garis sumbu adalah setengah dari panjang sisi dasar.
Sifat ini dapat dibuktikan menggunakan konsep kesebangunan segitiga. Jika kita bagi segitiga menjadi dua bagian yang sama besar oleh Garis Sumbu Adalah, maka kedua bagian yang dihasilkan adalah segitiga yang sebangun dengan segitiga asli.
Karena kedua segitiga tersebut sebangun, maka perbandingan sisi-sisi yang bersesuaian adalah sama. Salah satu perbandingan sisi yang bersesuaian adalah antara panjang garis sumbu dan setengah dari panjang sisi dasar.
Dengan demikian, dapat disimpulkan bahwa panjang garis sumbu adalah setengah dari panjang sisi dasar. Sifat ini sangat berguna dalam berbagai aplikasi, seperti menghitung luas dan keliling segitiga.
Sejarah
Garis Sumbu Adalah pertama kali ditemukan oleh matematikawan Yunani kuno, Euclid, pada abad ke-3 SM. Penemuan ini dicatat dalam buku Euclid yang terkenal, “Elements”. Dalam buku ini, Euclid menyajikan serangkaian aksioma, definisi, dan teorema yang membentuk dasar geometri.
Garis Sumbu Adalah merupakan salah satu konsep dasar yang diperkenalkan oleh Euclid dalam “Elements”. Euclid menggunakan garis sumbu untuk membuktikan berbagai teorema geometri, termasuk teorema Pythagoras. Teorema ini menyatakan bahwa kuadrat panjang sisi miring segitiga siku-siku sama dengan jumlah kuadrat panjang kedua sisi lainnya.
Penemuan Garis Sumbu Adalah oleh Euclid merupakan tonggak penting dalam perkembangan geometri. Konsep ini telah digunakan selama berabad-abad untuk memecahkan berbagai masalah geometri dan untuk mengembangkan teori geometri baru.
Aplikasi
Garis Sumbu Adalah memiliki peran penting dalam menyelesaikan berbagai masalah geometri, termasuk mencari luas dan keliling segitiga. Berikut adalah beberapa contohnya:
- Mencari luas segitiga: Luas segitiga dapat dicari menggunakan rumus: Luas = (1/2) x alas x tinggi. Garis Sumbu Adalah dapat digunakan untuk menentukan tinggi segitiga, yang merupakan jarak dari titik puncak ke sisi dasar. Mengetahui panjang garis sumbu dan setengah dari panjang sisi dasar, luas segitiga dapat dihitung dengan mudah.
- Mencari keliling segitiga: Keliling segitiga dapat dicari menggunakan rumus: Keliling = sisi1 + sisi2 + sisi3. Garis Sumbu Adalah dapat digunakan untuk menentukan panjang salah satu sisi segitiga, yaitu setengah dari panjang sisi dasar. Mengetahui panjang ketiga sisi segitiga, keliling segitiga dapat dihitung dengan mudah.
Selain itu, Garis Sumbu Adalah juga dapat digunakan untuk menyelesaikan berbagai masalah geometri lainnya, seperti:
- Mencari titik berat segitiga
- Membagi segitiga menjadi dua bagian yang sama besar
- Membuktikan teorema geometri
Dengan demikian, Garis Sumbu Adalah merupakan konsep penting dalam geometri yang memiliki berbagai aplikasi dalam menyelesaikan masalah geometri.
Pertanyaan Umum
Berikut adalah beberapa pertanyaan umum mengenai Garis Sumbu Adalah beserta jawabannya:
1. Apa itu Garis Sumbu Adalah?
Garis Sumbu Adalah adalah garis yang menghubungkan titik puncak segitiga dengan titik tengah sisi dasarnya. Garis ini membagi segitiga menjadi dua bagian yang sama besar.
2. Apa fungsi Garis Sumbu Adalah?
Fungsi utama Garis Sumbu Adalah adalah untuk membagi segitiga menjadi dua bagian yang sama besar. Selain itu, Garis Sumbu Adalah juga dapat digunakan untuk menentukan titik berat segitiga.
3. Bagaimana cara menentukan panjang Garis Sumbu Adalah?
Panjang Garis Sumbu Adalah sama dengan setengah dari panjang sisi dasar segitiga.
4. Siapa yang pertama kali menemukan Garis Sumbu Adalah?
Garis Sumbu Adalah pertama kali ditemukan oleh matematikawan Yunani kuno, Euclid, pada abad ke-3 SM.
5. Apa saja aplikasi Garis Sumbu Adalah?
Garis Sumbu Adalah memiliki berbagai aplikasi dalam geometri, seperti mencari luas dan keliling segitiga, membagi segitiga menjadi dua bagian yang sama besar, dan membuktikan teorema geometri.
Kesimpulan
Garis Sumbu Adalah merupakan konsep penting dalam geometri yang memiliki peran penting dalam menentukan sifat-sifat dan karakteristik segitiga. Garis ini membagi segitiga menjadi dua bagian yang sama besar dan memiliki sifat-sifat unik, seperti tegak lurus terhadap sisi dasar dan melalui titik berat segitiga. Garis Sumbu Adalah juga memiliki berbagai aplikasi dalam memecahkan masalah geometri, seperti mencari luas, keliling, dan titik berat segitiga.
Pemahaman yang mendalam tentang Garis Sumbu Adalah sangat penting bagi siswa, mahasiswa, dan siapa saja yang ingin mempelajari geometri secara menyeluruh. Konsep ini menjadi dasar untuk memahami sifat-sifat segitiga dan memecahkan berbagai masalah geometri dengan lebih mudah dan efisien.